Two-Film Theory and Equilibrium Solubility Curve
In the analysis of gas absorption, we are interested in the transfer of materials throughout the entire gas absorption equipment, not just a single location in the equipment. Therefore the two-film theory can be analyzed more effectively by using the equilibrium solubility curve.
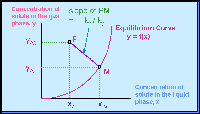
The concentrations at the interface in the gas ( yAi ) and in the liquid ( xAi ) is represented as a point M on the equilibrium solubility curve. Point M thus has the coordinates ( yAi, xAi ). As we move along the column along the continuous interface, we can trace out an equilibrium curve.
[ Remember that one of the assumptions of the two-film theory is that equilibrium condition exists at the interface ]
[ A number of other theories have also been used, e.g. penetration theory, surface-renewal theory, surface-stretch theory, etc. See pp.144-150, J.D. Seader & E.J. Henley, "Separation Process Principles" for more information. ]
Very often, the subscript "Ai" is dropped, and the equilibrium curve
is simply a relationship between y and x; i.e. y = f(x).
The concentrations in the bulk gas phase ( yAG ) and in the bulk liquid phase ( xAL ) is represented as a point P above the equilibrium curve. Point P thus has the coordinates ( xAL, yAG ). Point P is located above the equilibrium curve.
[ Remember that it is the departure from equilibrium that provide the driving force for mass transfer ]
See the Figure below :
Notation :
yAG = composition of A in the bulk gas phase (mole fraction)
xAL = composition of A in bulk liquid phase (mole fraction)
( xAi, yAi ) = equilibrium interface compositions (mole fraction)
Analysis of Mass Transfer Process using Two-Film Theory
In the gas-phase, the concentration falls from yAG in the bulk gas to yAi at the interface. Thus, there is a concentration driving force for mass transfer from the bulk gas to the gas film to the interface.
At the interface, the component A crossed the interface and enters the liquid side.
In the liquid-phase, the concentration falls from xAi at the interface to xAL in the bulk liquid. Thus, there is a concentration driving force for mass transfer from the interface to the liquid film to the bulk liquid.
The mass transfer process can be represented by the line PM. See the Figure above.
Mass transfer can be described by a set of mass transfer equations. Click here for more information.
NOTE : The bulk concentrations yAG, xAL are not equilibrium values, otherwise there would be no diffusion of A.
REMINDER :
The two-film theory and equilibrium curve can
be expressed in other ways, e.g. in terms of partial pressure (for the gas phase)
and concentration (for the liquid phase); but the analysis for them is the same
as outlined before for mole fractions ( x and y).
Refer to the Figure
below which showed the two-film theory and equilibrium curve expressed in partial
pressures and concentrations.