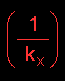 represents
the resistance to mass transfer in the liquid
phase
represents
the resistance to mass transfer in the liquid
phase
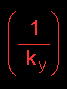 represents
the resistance to mass transfer in the gas
phase
represents
the resistance to mass transfer in the gas
phase
Mass Transfer Resistance
The resistance to mass transfer is defined as the reciprocal of the mass transfer coefficient:
represents the resistance to mass transfer in the liquid phase
represents the resistance to mass transfer in the gas phase
[Again, refer to the analogy with heat transfer whereby 1/h is the convective resistance to heat transfer]
It is important to know if one of the 2 resistances is controlling the mass transfer. If so, the rate of mass transfer can be increased by promoting turbulence in and/or increasing the dispersion of the controlling phase. Click here for more information.
Analysis of mass transfer resistance at a point P
From the 2 mass transfer equations, by rearranging and eliminating NA :
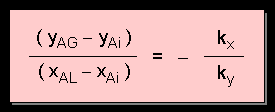
Referring back our analysis of mass
transfer from Point P to Point M, we see that the ratio
of mass transfer coefficients is actually equal to the slope
of line PM. The gradient of the line determines the relative resistances
of the 2 phases.
The above equation is useful if one does not know the interface equilibrium concentrations.
We can use the above equation to determine the equilibrium concentration at the interface ( xAi, yAi ), i.e. to locate point M, provided that kx and ky are known (or can be calculated using appropriate correlations). We do so by plotting a straight line originating from point P ( xAL, yAG ) with slope - kx / ky. The point of intersection of this line with the equilibrium curve gives point M which yield the values of xAi and yAi . That way we can calculate the flux NA at that particular point.